Fibonacci Dizisi, her sayının kendisinden bir önceki sayı ile toplanması ile elde edilen sayılar serisidir. Fibonacci Disizinde yer alan rakamların özelliği, Fibonacci Dizisinde yer alan sayıların kendilerinden bir öncekiyle oranlandığında oluşan serinin altın orana yaklaşarak ilerlemesidir.
Fibonacci dizisi 1 rakamı ile başlamak zorunda değildir. Herhangi bir rakam ile başlayabilir.
Örn/ 0-1-1-2-3-5-8-13-bir Fibonacci Dizisidir ancak Fibonacci Dizisi, 4-4-8-12-20-32-52-84 olarak da devam edebilir.
Fibonacci Dizisine neden Fibonacci Dizisi Denilir ?
Fibonacci Dizisi Leonardo Fibonacci tarafından bulunmuştur. İtalya’da doğmuş olan Leonardo Fibonacci bir problemi araştırırken bu sayıları keşfeder ve kendi adını vermeye karar verir.
Fibonacci Dizisi Neden Bu Kadar Önemlidir ?
Fibonacci Dizisi Nedir başlığında da bahsettiğimiz gibi, dizideki sayıların kendinden önceki sayıya bölünmesiyle altın orana yaklaşılması ve altın oranın da hayatımızdaki objelerin içinde yer alması bu sayıları önemli ve gizemli kılmıştır. Fibonacci Dizisinde yer alan altın oran, eski Mısırlılar bulmuşlardır. Yunanlılar da, Mısırlılar gibi bu sayıyı mimaride kullanmışlardır. Altın oranı basitçe anlatmak gerekirse,
Bütünü oluşturan parçalar arasındaki geometrik orandır.
Günlük hayatımızdan örnekler ile Fibonacci Dizisini açıklamaya çalışırsak,
İşaret parmağımızın bir önceki boğum ile oranı altın oranı vermektedir.
Fibonacci Dizisi ile ulaşabildiğimiz altın oran insan yüzündeki duyu organlarının oranlamasıyla da ortaya çıkmaktadır. Örneğin, kulaklarımızın, burnumuzun altından çenemize kadar olan alan altın oranı içermektedir.
Mısır Piramitlerinde de tabanının yüksekliğine oranı altın oranı vermektedir.
Fibonacci Dizisinin Finans Sektöründe Kullanımı
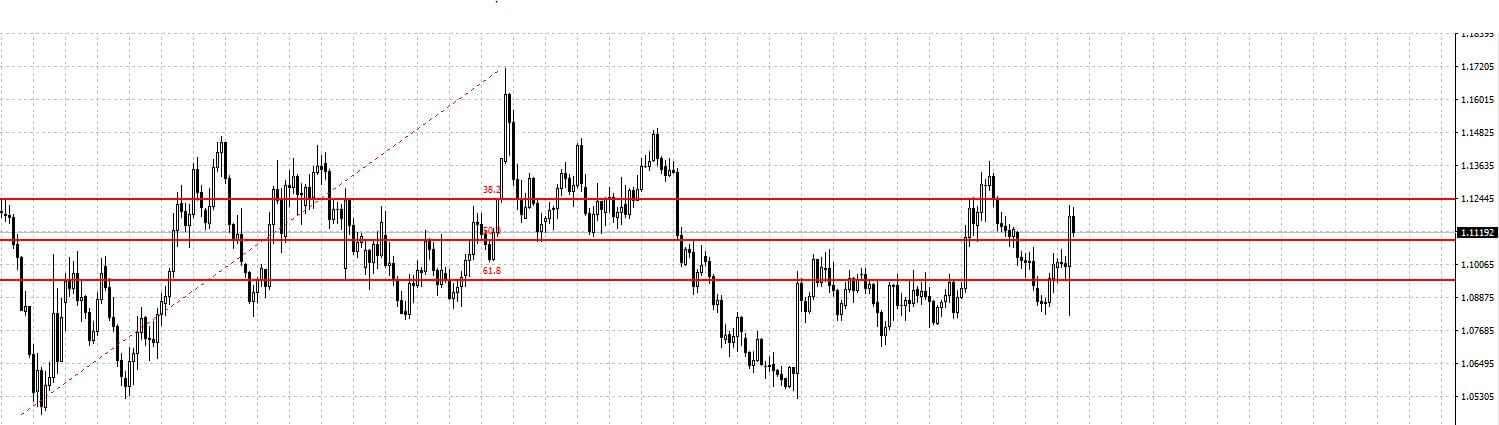
Fibonacci Düzeltme Seviyeleri ( Retracement )
Fibonacci Dizisi finans sektöründe finansal varlıkların alacakları değeri tahminlemede kullanılır. Teknik analiz uygulamalarında kullanılan Fibonacci Dizisi ile ulaşabileceğimiz altn orandır. Genel olarak kullanılan oranlar, 1.618 ve 1.232’dir.
ÖRN/ Baz aldığımız zaman aralığında en düşük fiyatı 1,0520, en yüksek fiyatı ise 1,1376 seviyesini görmüş olan bir pariteyi ele alalım.
Yüksek fiyat ile düşük fiyatı birbirinden çıkarttığımızda, 1,1376 – 1,0520 = 0,0856 olacaktır. Bu değeri yukarıdaki 1.272 ile çarptığımızda, 0,0856 * 0.232 = 0,0198 olacaktır. Bu değeri yüksek fiyat olan 1,1376’ ya eklediğimizde, 1,1578 olacaktır. Bu ortaya çıkan değer paritenin yükselmesini beklediğimiz trendi ortaya koyar.
.png)
Bu örnekten de anlaşılabileceği gibi, finans sektöründe bir paritenin hareketinin kesintisiz oluşması beklenemez. Fibonacci Dizisi bu trendi belirlememizde yardımcı olabilecek analizler sunmaktadır.
Fibonacci Dizisi’nin finans sektöründe bir diğer kullanımı da Fibonacci Zaman Aralıkları’dır.
Fibonacci Zaman Aralıkları Nedir ?
Yukarıda bahsettiğimiz analiz yöntemlerindeki tek değişken fiyat değildir. Zaman değişkenin de kapsamlı olarak incelenmesi gereklidir. Bu bağlamda Fibonacci Dizileri fiyat değişimlerinde kullanıldığı gibi zaman aralıklarında da kullanılabilir. Zaman aralıkları belirlenirken Fibonacci Dizisi’ndeki rakamlar gün olarak baz alınır yani, 1-1-2-3-5-8-13-21-34 şeklinde trend gün aralıklarına bölünür. Bu analiz dalgalanmaların süresini tespit etmekte kullanılmaktadır.
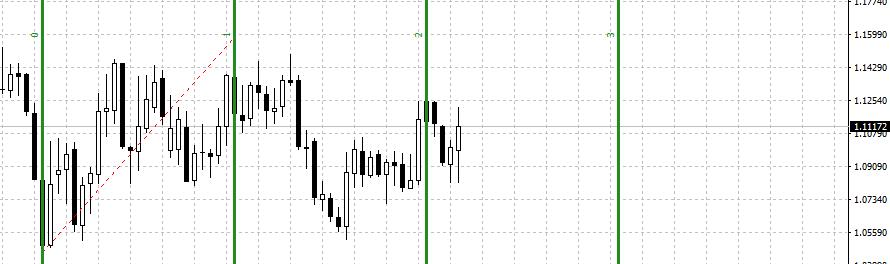
Fibonacci Yayları Nedir ?
Fibonacci Yayları paritenin izlediği trendin taban seviyesinden tavan seviyesine çizilen referans çizgisi ile oluşturulur. Bu çizginin %81.8, %50 ve %38.2 seviyelerine çizilen yaylara Fibonacci Yayları denir.
Fibonacci Yayları analiz yönteminde fiyat yaya yukarıdan yaklaşıyorsa destek, aşağıdan yaklaşıyorsa direnç olarak yorumlanır.
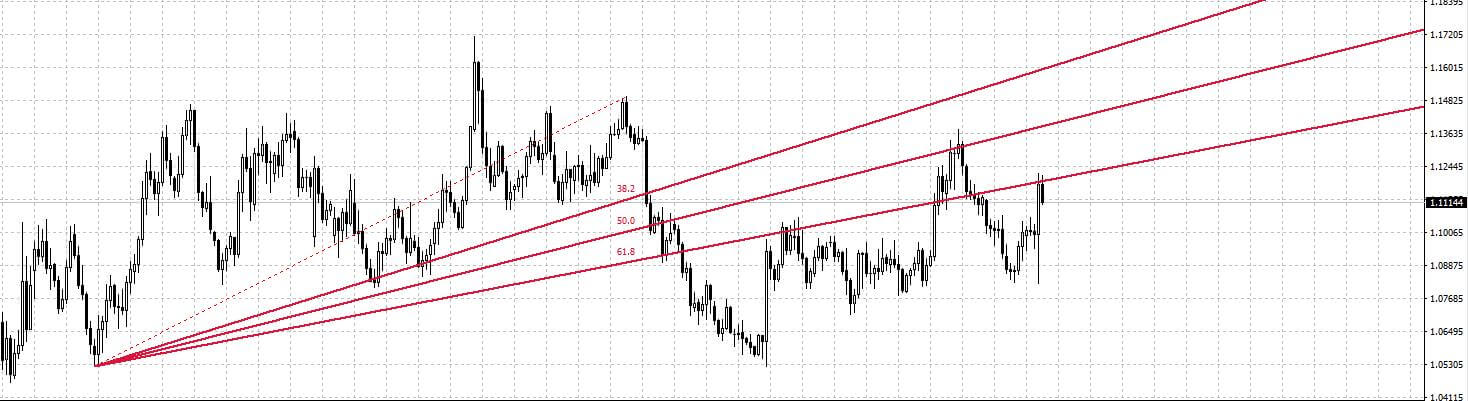
Fibonacci Fanları Nedir ?
Fibonacci Dizisi’nin finansal analizlerdeki diğer kullanım alanı da, Fibonacci Fan Çizgileridir.
Diğer Fibonacci Analizlerinde de bahsettiğimiz gibi Fibonacci Fanlarında da taban ve tavan noktalarına klavuz çizgi çizilir. Bu klavuz çizgi ana trendin değil ara trendin tavan noktasına çizilmelidir.
Fibonacci Fan Analizi doğruluğu kesinleşmiş bir analiz yöntemi değildir. Bunun sebebi, volatil piyasalarda ya da dönemlerde yanılma payının artmasıdır. Bu sebeple daha istikrarlı stabil piyasalarda uygulanması önerilir.